CircuitGenerators Module
This file implements functions for generating computer arithmetic ciruits. The overall idea is that the circuit is generated as a side effect when calling a generator function with input bitvectors. The generator function is thereby given the input and output bitvectors as string[]. This way, also circuits for arithmetic expressions can be generated.
Types
Functions and values
| Function or value | Description | |||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
AddNewGateWithOutputNames outputs g
Parameters:
string[]
g : CircuitGate
Returns: string[]
|






AddNewGateWithOutputNames adds gate g to the background circuit; if it was already there, it returns the output wire names, otherwise it uses the given ones as names of the outputs of the gate
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
Batc68Concentrator rmMSB x
Parameters:
bool
x : string[][]
Returns: string[][]
|






This concentrator is derived from Batcher's bitonic sorting network by just comparing the most significant address bits, and removing these from the outputs in case rmMSB is true (so that the next bits are considered in the next stage of the radix-based sorting network). It leads to a binary sorter of depth O(log(n)^2) and size O(nlog(n)^2). See also
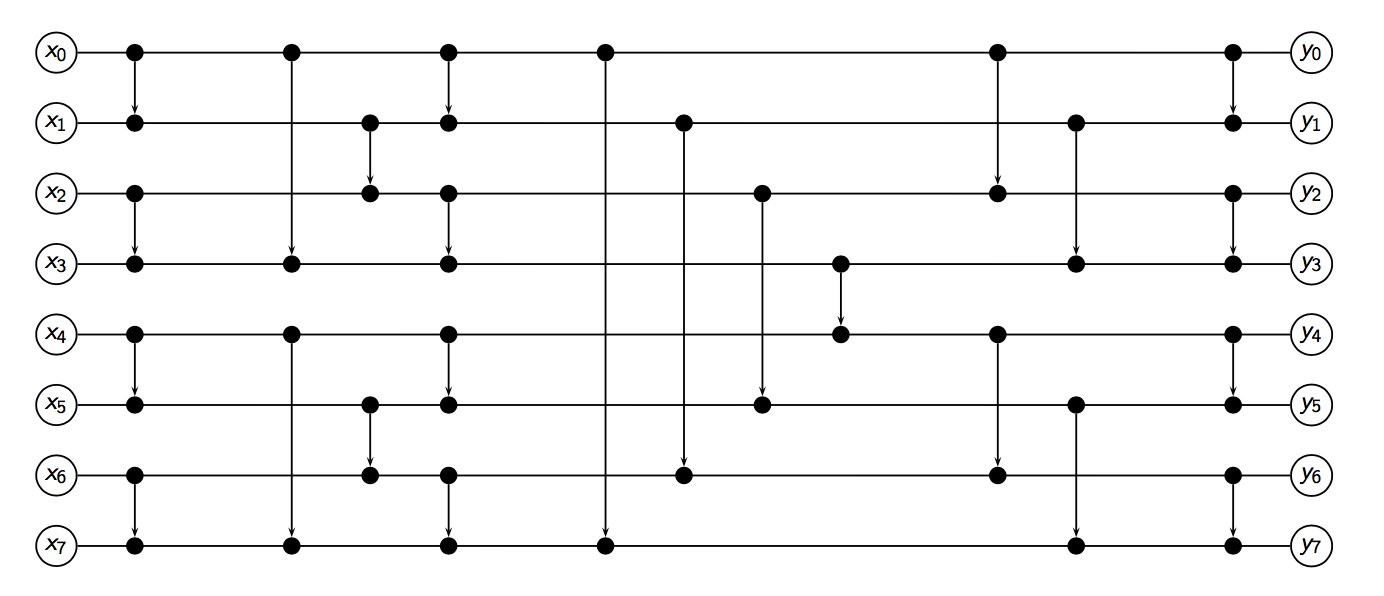
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
BatcherBanyan x
Parameters:
string[][]
Returns: string[][]
|






This circuit implements a Batcher-Banyan network (see [Nara88]) which consists of a (Batcher) sorting network that sorts the inputs by their addresses
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
BitonicMerger addCmpSwap inputs
Parameters:
string[] * string[] -> string[] * string[]
inputs : string[][]
Returns: string[][]
|






This circuit implements Batcher's bitonic merge network that is based on a network with compare-and-swap modules which are combined in half cleaners. Essentially, Batcher's bitonic merge network is a binary tree whose nodes are half cleaners whose width is doubled in each level of the tree (the leftmost half cleaner in the root node should reverse the second half of its input which is done in the call in BitonicSorter). See also
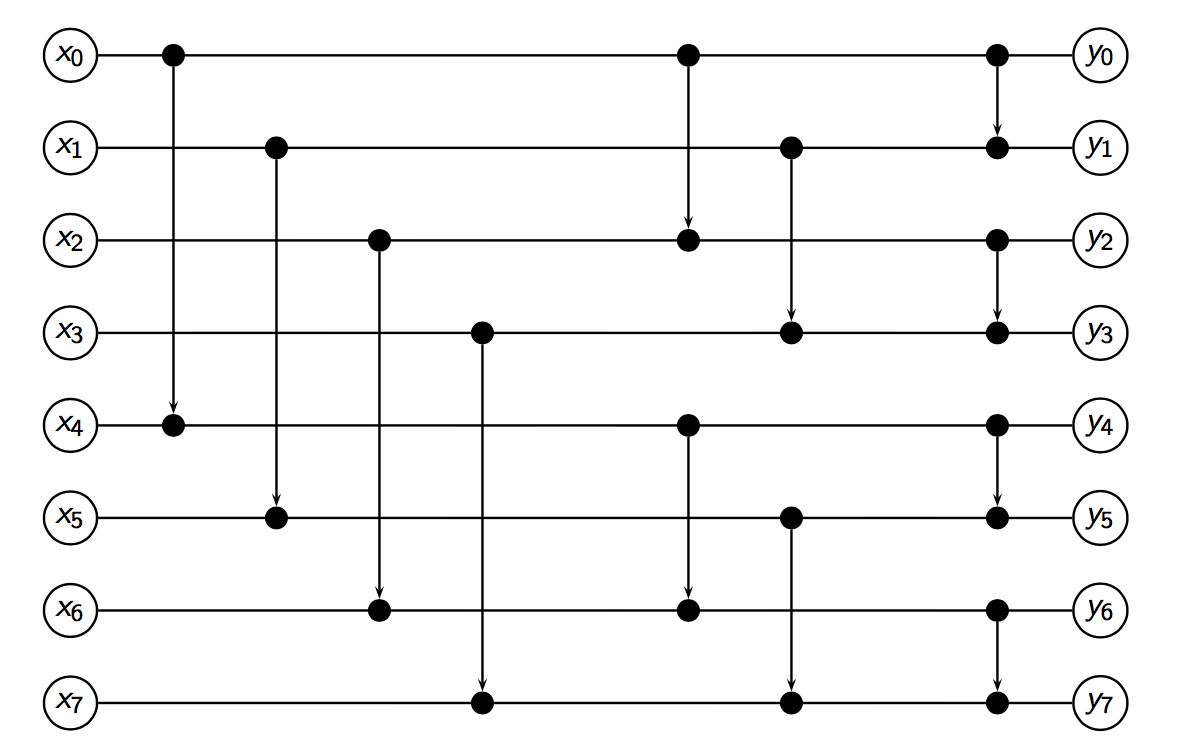
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
BitonicSorter addCmpSwap x
Parameters:
string[] * string[] -> string[] * string[]
x : string[][]
Returns: string[][]
|






This circuit implements Batcher's bitonic sorting network that is based on the merge sort paradigm, i.e., first splitting the given list into halves, sorting these recursively with the same algorithm, and then merging the sorted halves into a single sorted list. The merging step is done here by Batcher's bitonic merge network (function BitonicMerger) where however the second half of its input has to be reversed to obtain a bitonic sequence. See also

|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
ChCh96Concentrator rmMSB x
Parameters:
bool
x : string[][]
Returns: string[][]
|






This concentrator is defined in [ChCh96] and recursively implements a binary sorter that is based on the observation that all internal vectors can be made compact vectors in the sense that all 1s in these vectors occur as a contiguous sequence. The concentrator is based on the generalized cube network which is the BY-BF-FS (banyan/butterfly network with outgoing flip shuffle permutation). The network used is isomorphic to the Omega-network and also to Batcher's bitonic merger.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
ChOr94Concentrator rmMSB x
Parameters:
bool
x : string[][]
Returns: string[][]
|






This concentrator is defined in [ChOr94] and implements recursively a binary sorter using the parallel merge sort paradigm (see ChOr94Merger). Hence, the given input vector is split into two halves which are sorted recursively, and are then merged by ChOr94Merger for n>2. See also function ChOr94Merger and
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
ChOr94Merger isFinal x
Parameters:
bool
x : string[][]
Returns: string[][]
|






This concentrator is defined in [ChOr94] and implements recursively a binary sorter using the parallel merge-sort paradigm. Merging is done here for so-called bi-sorted binary sequences, i.e., sequences whose two halves are sorted sequences. The merging circuit used in the design is able to merge two bi-sorted sequences into a single sorted sequence. This is done by the observation that if two sorted binary lists xUpp and xLow are split into halves, i.e., xUpp=x1*x2 and xLow=x3*x4, then two of these halves are clean, i.e. contain only 0s or only 1s, and the other two halves are sorted. The merging circuit has to identify the clean and the sorted quaters and forwards the sorted quarters to a recursive merge module. Finally, it concatenates the already clean quarters with the sorted result of the recursive call. See also
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
CheckConcentrator checkSorter checkTernary checkRBS circ
Parameters:
bool
checkTernary : bool
checkRBS : bool
circ : LeveledCircuit
Returns: (Map<string, bool> * int[] * int[]) option
|






Checking the correctness of a binary/ternary sorter/concentrator: The function simulates the given LeveledCircuit for all possible inputs and will check whether it is a binary/ternary sorter/concentrator. The result will be an optional tuple (env,xVec,yVec) holding a potential counterexample where 0,1,2 means 0,⊥,1 in ternary and 0,1 obviously means 0,1 in binary. For binary inputs, all bits of an input are constant so that 2**n vectors have to be checked. Their length is log2(n)+1 since we use one message bit. Ternary inputs look like |v0;v1;|v0|v1...v1| using two message bits, one validity bit v0, and log(n) address bits. If input checkSorter holds, it is checked that the output sequence is of the form 0..0⊥..⊥1..1, and otherwise, it is checked that it is a concentrated vector, i.e., 0s are only allowed in the upper half if the lower half is full of 0s, and 1s are only allowed in the lower half if the upper half is full of 1s. Finally, if checkRBS is true, then all input vectors are ignored where the number of 0s or the number of 1s exceeds n/2.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
CheckFunction genCircuit checkFun n1 n2
Parameters:
string[] -> string[] -> string[]
checkFun : bool[] -> bool[] -> bool[] -> bool
n1 : int
n2 : int
Returns: (bool[] * bool[] * bool[]) list
|






Check correctness of an arithmetic circuit generator genCircuit: This function will generate all bitvectors with n1 and n2 bits, respectively, as arguments, and will then evaluate the circuit on all input vectors. It then checks whether the given function checkFun yields true when given the input and output bitvectors.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
CheckInterconnectionNetworkPartial circ
Parameters:
LeveledCircuit
Returns: (int option[] * Map<string, bool>) option
|






Checking whether an interconnection network given as a circuit can route all partial permutations correctly. The function simulates the circuit with all partial permutations where the circuit with n inputs is expected to have inputs x[i] with 2*(log2 n)+1 bits since the target address will have log2(n) bits, and it is also used as the message for each x[i]. Morever, each input has a valid bit so that each x[i] consists of the message x[i][0..q-1]*x[i][q]*x[i][q+1..2q+1] with q:=log2(n). Note that the number of partial permutations of n objects is given as sum_{i=0}^{n} i!*binom(n,i)^2 (see function Global.PartialPermutations). The result is an optional pair (perm,env) where perm is the input vector of type (int option)[], and env the variable environment obtained by the simulation in case a counterexample has been found. If the circuit correctly routes all partial permutations the result is None.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
CheckLeveledCircuit c spec
Parameters:
LeveledCircuit
spec : bool[][] -> bool[][] -> bool
Returns: Map<string, bool> list
|






This function verifies a given leveled circuit in that it simulates it on all possible inputs and checks whether the given F# function spec satisfies the input/output combination. It returns all variable assignments where the specification failed.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
CheckRankingCircuit firstRank rankGen n
Parameters:
int
rankGen : string[] -> string[][]
n : int
Returns: bool[] list
|






checking the correctness of a ranking circuit that starts with firstRank for the first valid entry (RankingTree0 needs 1, others 0), e.g. you may use this as follows
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
Circuit2Bdds garbageCollect circ
Parameters:
bool
circ : LeveledCircuit
Returns: int[][]
|






Compute BDDs for the outputs of a given circuit. The function retains also all BDDs that have been computed for the internal wires of the circuit and could be optimized in that these are put into the garbage when no longer needed. If optFlag is true, the function will do garbage collection after every level of the circuit.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
ComputeComplexity c
Parameters:
LeveledCircuit
Returns: int * int * int * int * int * int * int * int * int * int * int
|






Compute complexity measures of a leveled circuit: This function returns a tuple (depth,numAND,numXOR,numOR,numHA,numFA,numPG,size) where all components have the obvious meaning, and size is the gate count in terms of 2-input, 1-output gates (where HA, FA, PG, SW are expanded to 2, 5, 3, and 8 gates, respectively).
|
|||||||||||||||||||||||||||||||||||||||||||||||
|






main function to be called by the ComputerArithmeticCircuitGenerateTool on the teaching tool web page
|
|||||||||||||||||||||||||||||||||||||||||||||||
|






main function to be called by the ComputerArithmeticCircuitVerifyTool on the teaching tool web page to verify a given arithmetic circuit
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
Crossbar mkPartial x
Parameters:
bool
x : string[][]
Returns: string[][]
|






This generator constructs a crossbar circuit that can connect anyone of its n inputs with anyone of its n outputs as long as the mapping of the inputs to the outputs is a (partial) permutation. To this end, the n input vectors consist of q=x[i].Length-log2(n) bits of the message concatenated with log2(n) bits of the target address. Note that we do not have to distinguish partial permutations here.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
EnumerateBitvectors n
Parameters:
int
Returns: bool[] list
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
EvaluateLeveledCircuit varAssign c
Parameters:
Map<string, bool>
c : LeveledCircuit
Returns: Map<string, bool>
|






Evaluate a leveled circuit based on a variable assignment varAssign that initially only holds values for the input variables. Based on these input values, the function evaluates each level and adds the values of all variables to the variable assignment that is finally returned.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
GetLeveledCircuit name inputs outputs
Parameters:
string
inputs : string[][]
outputs : string[][]
Returns: LeveledCircuit
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
HalfCleanerBinaryOpt sortGen rmMSB x
Parameters:
bool -> string[][] -> string[][]
rmMSB : bool
x : string[][]
Returns: string[][]
|






The following function takes a generator sortGen for a binary sorter and constructs a binary concentrator of it by using two sorters of half the size and a further half cleaner column as reported in [KoOr90,Nara88] and explicitly in [JaSc18,JaSJ17b]. The construction is therefore as follows:
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
HalfCleanerTernaryOpt sortGen rmMSB x
Parameters:
bool -> string[][] -> string[][]
rmMSB : bool
x : string[][]
Returns: string[][]
|






The following function takes a generator sortGen for a ternary sorter and constructs a concentrator of it by generating two sorters of half the size and a further half cleaner column as reported in [KoOr90,Nara88] and explicitly in [JaSc18,JaSJ17b]:
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
InValidIntCntComb (modName, aryName, optName, cncName)
Parameters:
string
aryName : string
optName : string
cncName : string
Returns: bool
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
IntAddCLA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






The function adds gates for a carry-lookahead addition of 2-complement numbers x1 and x2 of the same length n and returns the n+1 bits of the sum bitvector.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
IntAddCRA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






The function adds gates for a carry-ripple addition of 2-complement numbers x1 and x2 of the same length n and returns the n+1 bits of the sum bitvector.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
IntMulCRA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






IntMulCRA is a simple paper-and-pencil multiplier for 2-complement numbers that adds up the partial products row by row using carry-ripple adders.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
IntSubCLA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






The function adds gates for a carry-lookahead subtraction of 2-complement numbers x1 and x2 of the same length n and returns the n+1 bits of the sum bitvector.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
IntSubCRA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






The function adds gates for a carry-ripple subtraction of 2-complement numbers x1 and x2 of the same length n and returns the n+1 bits of the sum bitvector.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
InterconnectComplexityPrintLatex fileName q minLN maxLN
Parameters:
string
q : int
minLN : int
maxLN : int
|






This function prints the contents of InterconnectComplexity in Latex tables and plots; the results are printed both on the screen and are also written in the specified file for the given number of message bits q and numbers of inputs n=2^minLN .. 2^maxLN
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
InterconnectComplexityTable
Returns: Map<(string * string * string * string * int * int), (int * int * int * int * int * int * int * int * int * int * int)>
|






this is a global table to store the complexity results (so that new results can be incrementally added by need) keys are tuples (modName,aryName,optName,cncName,q,n) and values are tuples (depth,nNOT,nAND,nXOR,nOR,nHA,nFA,nPG,nMX,nSW,size)
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
InterconnectComplexityTableAdd q minLN maxLN
Parameters:
int
minLN : int
maxLN : int
Returns: Map<(string * string * string * string * int * int), (int * int * int * int * int * int * int * int * int * int * int)>
|






This function adds new results to InterconnectComplexityTable: For q message bits, and n=2^minLN .. 2^maxLN, it generates all possible concentrators and radix-based interconnection networks and adds their cmplexity results to InterconnectComplexityTable
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
InterconnectComplexityTableGetDepthFormulas q minLN maxLN
Parameters:
int
minLN : int
maxLN : int
|






This function reads the data about the depth from the complexity table InterconnectComplexityTable and computes a polynomial for the last 4 points that satisfies D(n) = sum_{i=0}^3 c[i]*log(n)^i
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
JaSJ17Concentrator rmMSB x
Parameters:
bool
x : string[][]
Returns: string[][]
|






This circuit generator is a parallel version of Narasimha's concentrator [Nara94] that is published in [JaSJ17]: As Narasimha's concentrator, this circuit is based on a RB-FS-RV permutation network (reverse banyan/ flip shuffle with reverse output permutation) and configures switch i of each column by the parity of the input vector's prefix x[0..2i], so that half of the 0s in x[0..2i+1] are send to the lower and upper subnetworks (same with the 1s since each prefix x[0..2i+1] consists of an even number of inputs). In case that the prefix x[0..2i+1] contains an odd number of 0s (and therefore also an odd number of 1s, the additional 0 is sent to the lower and the additional 1 is sent to the upper subnetwork. See also The difference between JaSJ17 and Nara94 is that the computations of the parity bits to configure the switches in JaSJ17 is done by a parallel prefix tree that reduces the depth of the concentrator from O(n) to only O(log(n)^2).
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
KoOr90Concentrator rmMSB x
Parameters:
bool
x : string[][]
Returns: string[][]
|






Koppelman-Oruc-like Concentrator [KoOr90], i.e., binary sorting by first computing ranks and then self-routing by using the ranks as local target addresses. This version of the KoOr90 idea first computes the ranks of the 0s (by ranking the negated inputs) so that it can also be used with RadixBasedTernaryInterconnect to implement partial permutations. For routing the 0s to their local target address, i.e., their rank, we use a RB-FS-RV (reverse-banyan/flip-shuffle network with reverse output) permutation network, as used in Nara94 and JaSJ17 whose configuration is however determined in a different way using the ranks: Inputs are partitioned by the least significant bit of their rank. So, we first obtain two partitions with rank ...0 rank ...1, and after that, we have four partitions with ranks ...00, ...10, ...01, and ...11. In each stage, each group is split into two further groups with new address bits 0 and 1, respectively. Finally, we obtain for example for 8 inputs the ranks 000, 100, 010, 110, 001, 101, 011, and 111 so that the reverse output permutation (reversing the address bits) will map them to the right output.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
MkInterconnectCircuit modName aryName optName cncName q n
Parameters:
string
aryName : string
optName : string
cncName : string
q : int
n : int
Returns: LeveledCircuit
|






This function will generate either a concentrator/sorter or an entire interconnection network based on radix-based sorting. It combines all other generator functions for concentrators and RBS interconnection networks including their optimization by half cleaners. To this end, the following inputs are expected:
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
Nara94Concentrator rmMSB x
Parameters:
bool
x : string[][]
Returns: string[][]
|






This circuit generator constructs Narasimha's concentrator [Nara94] which is actually a binary sorter: The circuit is based on a RB-FS-RV permutation network (reverse banyan/flip shuffle with reverse output permutation) and configures switch i of each column by the parity of the input vector's prefix x[0..2i], so that half of the 0s in x[0..2i+1] are send to the lower and upper subnetworks (same with the 1s since each prefix x[0..2i+1] consists of an even number of inputs). In case that the prefix x[0..2i+1] contains an odd number of 0s (and therefore also an odd number of 1s, the additional 0 is sent to the lower and the additional 1 is sent to the upper subnetwork. See also
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatAddCLA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






The function adds the gates for a carry-lookahead addition of radix-2 numbers x1 and x2 of the same length n and returns the n+1 bits of the sum bitvector.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatAddCRA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






The function adds the gates for a carry-ripple addition of radix-2 numbers x1 and x2 of the same length n and returns the n+1 bits of the sum bitvector.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatMulCRA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






NatMulCRA is a simple paper-and-pencil multiplier that adds up the partial products row by row using carry-ripple adders. The depth of a nxn multiplier is 3(n-1), the number of AND gates is n*n for the partial products, and n-1 half adders, and (n-1)^2 full adders are used.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatMulCSA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






NatMulCSA is a simple array multiplier that adds up the partial products row by row using carry-save adders and uses a carry-ripple adder at the end. The depth of a nxn multiplier is 2n-1, the number of AND gates is n*n for the partial products, and n-1 half adders, and (n-1)^2 full adders are used. Hence, the size is exactly the same as NatMulCRA, but the depth is reduced from 3(n-1) to 2n-1.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatMulDadda x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatMulGreedyFAHA onlyFA onlyHA x1 x2
Parameters:
bool
onlyHA : bool
x1 : string[]
x2 : string[]
Returns: string[]
|






NatMulGreedyFAHA reduces the columns of the partial products in a greedy way, i.e., all columns with more than 3 summands are reduced by using full adders and half adders. Inputs onlyFA and onlyHA can be used to restrict the reduction to full and half adders only (if both were true there is an infinite loop without reductions). While this multiplier is easiest to implement, it requires O(n) reduction steps if no half adders are used, and is therefore bad.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatMulWallace x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






NatMulWallace is based on Wallace's reduction of the summands in that groups of three rows are compressed to two rows using a CSA adder. This way, the number of rows row[i] for multiplying n by m bits is defined as row[0] := m and row[j+1] := 2*(row[j] div 3) + (row[j] mod 3).
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatSubCLA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






The function adds the gates for a carry-lookahead subtraction of radix-2 numbers x1 and x2 of the same length n and returns the n+1 bits of the sum bitvector.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
NatSubCRA x1 x2
Parameters:
string[]
x2 : string[]
Returns: string[]
|






The function adds the gates for a carry-ripple subtraction of radix-2 numbers x1 and x2 of the same length n and returns the n+1 bits of the sum bitvector.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
ParPrefix1 f x n
Parameters:
'a -> 'a -> 'a
x : 'a[]
n : int
Returns: 'a[]
|






Parallel Prefix Computation (not work efficient): Given an array x[n..0] and an associative function f, ParPrefix1 computes an array p[n..0] such that p[i] = f(x[0..i]) with depth D(n) in O(log(n)) and work S(n) in O(n/2*log(n)) so that the algorithm is not work optimal. Note that D(n) := D(n/2)+1 and S(n) := 2*S(n/2)+n/2, which yields D(n) in O(log(n)) and S(n) in O(n/2*log(n)).
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
ParPrefix2 f x n
Parameters:
'a -> 'a -> 'a
x : 'a[]
n : int
Returns: 'a[]
|






Parallel Prefix Computation (work efficient): Given an array x[n..0] and an associative function f, ParPrefix2 computes an array p[n..0] such that p[i] = f(x[0..i]) with depth D(n) in O(log(n)) and work S(n) in O(n) so that the algorithm is work optimal. Note that D(n) := D(n/2)+2 and S(n) := S(n/2)+n-1, which yields for powers of 2 a depth of D(n)=2log(n) in O(log(n)) and S(n)=2(n-1)-log(n) in O(n) so that the algorithm is work optimal.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
ParseLeveledCircuitFromFile filename
Parameters:
string
Returns: LeveledCircuit
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
PrintGates ()
Parameters:
unit
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
PrintLeveledCircuit ostr env c
Parameters:
TextWriter
env : Map<string, bool> option
c : LeveledCircuit
|






print a levelized circuit to output stream ostr; if also a variable environment is given, the values of the variables in the circuit are printed as comments in each line of the definition of these variables.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
RadixBasedInterconnect split x
Parameters:
string[][] -> string[][]
x : string[][]
Returns: string[][]
|






This generator function constructs an interconnection network based on radix-based sorting. As inputs, it first requires a function split that maps an input array x[0..n-1] to an output array z[0..n-1] such that the lower half z[0..n/2-1] and upper half z[n/2..n-1] are treated recursively with the same function. Finally, the outputs of these recursive calls are appended.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
RadixBasedTernaryInterconnect split x
Parameters:
string[][] -> string[][]
x : string[][]
Returns: string[][]
|






This generator function constructs an interconnection network based on radix-based sorting that is capable of routing partial permutations [Nara94] for KoOr90, JaSJ17, and Nara94. As inputs, it first requires a function split that maps an input array x[0..n-1] to an output array z[0..n-1] such that the lower half z[0..n/2-1] and upper half z[n/2..n-1] should contain the inputs with most significant address bits 0 and 1, respectively. In contrast to RadixBasedInterconnect, a first binary sorter is used to sort the inputs by their validity bits, such that the invalid inputs appear after the valid ones. Then, the target addresses of the invalid inputs are set to zero so that a further radix-based sorting with a certain binary sorting algorithm will move the inputs with most significant address bit 1 through the invalid ones. If we cut the RBS-network after its leftmost splitter, we would obtain exactly the circuit generated by TernarySeqSorter. As can be seen there, the outputs will be sorted as 0...0⊥...⊥1...1 by their msbs. Thus, the special RBS-network used here will cut that output into two halves, and will reverse the second one, so that 0...0⊥...⊥ and 1...1⊥...⊥ are obtained. Removing the msb allows then to recursively continue this way. CAUTION: This construction does not work with arbitrary binary sorters, the used binary sorters must either be stable so that they never flip real 0s with ⊥s (that have also address bits 0) or where the output index of all prefixes x[0..i] are only determined by the values in that prefix. Examples for such prefix-defined binary sorting algorithms are KoOr90, JaSJ17 and Nara94.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
RankingTree0 x
Parameters:
string[]
Returns: string[][]
|






Generate a circuit for a ranking, i.e., a circuit with n boolean inputs x[0..n-1], and n outputs y[i] of length ceil(log2(n+1)) such that y[i] is the rank of each valid input x[i]. In case of this circuit, rank[i] is simply the number of 1s in the prefix x[0..i], thus the first 1 will have rank 1, the second 1 will have rank 2, etc. Rank entries rank[i] for x[i]=0 have no meaning. The maximal possible rank is thus n. The circuit uses a parallel prefix computation of depth 2*log(n)-1 with 2*n-log(n)-2 carry ripple adders. The width of the used adders is adapted to the maximal width of the expected numbers.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
RankingTree1 x
Parameters:
string[]
Returns: string[][]
|






Generate a circuit for a ranking, i.e., a circuit with n boolean inputs x[0..n-1], and n outputs y[i] of length ceil(log2(n)) such that y[i] is the rank of each valid input x[i]. In case of this circuit, rank[i] is simply the number of 1s in the prefix x[0..i] minus 1, thus the first 1 will have rank 0, the second 1 will have rank 1, etc. Rank entries rank[i] for x[i]=0 have no meaning. The maximal possible rank is n-1. The circuit uses a parallel prefix computation of depth 2*log(n)-1 with 2*n-log(n)-2 carry ripple adders. The width of the used adders is adapted to the maximal width of the expected numbers. This circuit is just derived by decrementing all ranks computed by RankingTree0.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
RankingTree2 x
Parameters:
string[]
Returns: string[][]
|






Generate a circuit for a ranking, i.e., a circuit with n boolean inputs x[0..n-1], and n outputs y[i] of length ceil(log(n)) such that y[i] is the rank of each valid input x[i] which means that the leftmost valid x[i] will have rank 0, the next one has rank 1 and so on. This ranking circuit works with 2-complement numbers where initially all bits are prepended with a "0" except for x[0] which will become [|"1";"1"|]=-1 and [|"0";"0"|]=0 for x[0]=0 and x[0]=1, respectively. Using these initial values, the same adder tree is applied as in the other ranking circuits of this module.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
ResetCircuit w
Parameters:
string
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
TernaryParConcentrator sortGen rmMSB x
Parameters:
bool -> string[][] -> string[][]
rmMSB : bool
x : string[][]
Returns: string[][]
|






This function (TRC) constructs a concentrator for ternary inputs using two binary sorters generated by sortGen. It is similar to TernaryParSorter, but does not make use of the multiplexers to select the 0s and 1s from the 0- and 1-sorter. Instead, it simply takes the lower half from the 0-sorter and the upper half from the 1-sorter, but remaps the 1 and 0 first back to ⊥ so that it will never take a 1 from the 0-sorter and never it will take a 0 from the 1-sorter (as TRP). However, this only works correctly if the numbers of 0s and 1s are less than or equal to n/2. If so, the circuit is even a ternary sorter, otherwise it is not even a correct concentrator.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
TernaryParSorter sortGen rmMSB x
Parameters:
bool -> string[][] -> string[][]
rmMSB : bool
x : string[][]
Returns: string[][]
|






This function (TRP) constructs a sorter for ternary inputs using two binary sorters generated by sortGen. The two binary sorters are thereby put in parallel where one (called the 1-sorter) considers ⊥ as 0 while the other one (called the 0-sorter) considers ⊥ as 1 for sorting. Hence, the 1-sorter's outputs 1 and the 0-sorter's outputs 0 are at the right places, so that the final output is obtained by taking the 1s from the 1-sorter and the 0s from the 0-sorter, leaving the remaining outputs ⊥.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Full Usage:
TernarySeqSorter sortGen rmMSB x
Parameters:
bool -> string[][] -> string[][]
rmMSB : bool
x : string[][]
Returns: string[][]
|






This function (TRS) constructs a sorter for ternary inputs using two binary sorters generated by sortGen. The two binary sorters are thereby put in sequence as shown below where the first sorter sorts the inputs according to their validity, i.e., it maps 0 and 1 to 1, and ⊥ to 0. After that, an input sequence {⊥}^j{0,1}^i is obtained that is then reversed so that a sequence of the form {0,1}^i{⊥}^j is given to the second sorter. The second sorter maps 0, and ⊥ to 0, and 1 to 1 so that the 1s must move through the ⊥s to abtain a sorted sequence 0^i ⊥^j 1^k.
|